Batch 2 - Class 78 - Compositions

• Instead of casting out nines, you can also cast out 11s. Start with the rightmost digit, and alternately add and subtract. So with 44689, you'd take 9-8+6-4+4=7. If you land up with a negative number, just add 11 as many times as required. Why does this process work, and can you use this to catch mistakes that you can't catch with casting out 9's?

  Why does this work? (Answer: Note that 1000=11*91-1; 100=11*9+1; 10=11*1-1 and so on)Catching mistakes - Casting out 11 can catch transpositions. For example, 7765=6313+1452. Both casting out 9's and 11's will check this. However, if a digit were transposed, i.e. 7675, then casting out 9's wont work but casting out 11's will. (Any idea on what kind of transpositions will it not catch?)

• List all the compositions of 1. Now try 2. Now try 3 (which you can just copy from the introduction up there!). Now try 4. How many compositions does it have? 
• Do you see a pattern here? Can you see why the pattern will continue that way? How many compositions will 10 have? 

  Answer: These are powers of 2. Why? Note that you can take each of the partition points, and either place a "+" there or not. Each such choice gives a different composition.
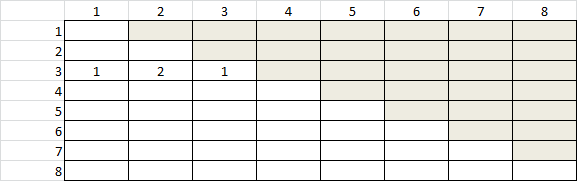
• Now we're going to organize our compositions by the size of the first part. For 3, we see that two of the compositions begin with 1, one composition begins with 2, and one with 3. Can you finish filling in the chart below? What patterns do you notice? Why do they occur?

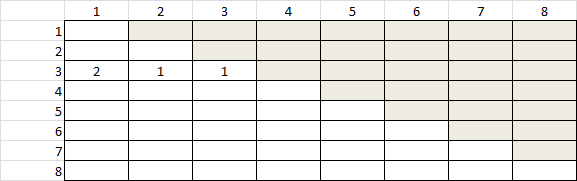
• Answer: 
• 

• If you look at all the compositions of a number, how many of them are made of only odd parts? For instance, some of the compositions of 5 that would work are 5, 1 + 3 + 1, and 1 + 1 + 1 + 1 + 1, but there are others. How many? 
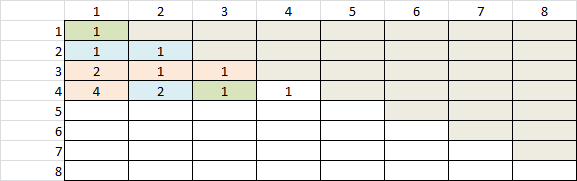
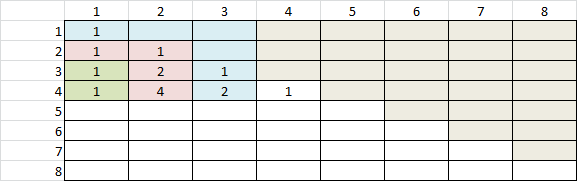
• Organize your compositions by the number of parts. In other words, for 3 we'd list that there is one composition with 1 part, two with 2 parts, and one with 3 parts. Do the same thing for the compositions of several other numbers, and hunt for patterns. Can you predict how many compositions of 8 have exactly 5 parts? 

• Answer: Its nC0, nC1, nC2 and so on - Why?
• Organize your compositions by the size of the largest part. For 3, we'd have one composition whose largest part is 3, two whose largest part is 2, and one whose largest part is 1. What patterns can you uncover now? Can you predict how many compositions of 8 have 3 as their largest part? 

• Answer: Can you think of it as choosing a first partition, and then applying recursion on previous choices?
• 

  
  

• (Dudeney - 44) Mr. and Mrs. Jorkins have fifteen children, all born at intervals of one year and a half. Miss Ada Jorkins, the eldest, had an objection to state her age to the census man, but she admitted that she was just seven times older than little Johnnie, the youngest of all. What was Ada's age? Do not too hastily assume that you have solved this little poser. You may find that you have made a bad blunder!

  Answer: 24 years (Little Johney is 3 years - its "seven times older" hence "eight times as old" - otherwise the answer would be 24.5 and 3.5)